- Teoria della Scienza Quantistica;
- Meccanica Statistica;
- Sistemi Dinamici.
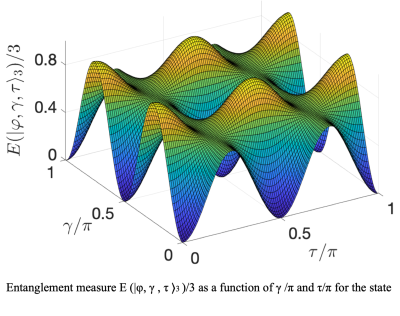
- Stima dell’entanglement quantistico.
- Stima della correlazione quantistica.
- Stati del grafo.
- Geometria dello spazio di Hilbert proiettivo.
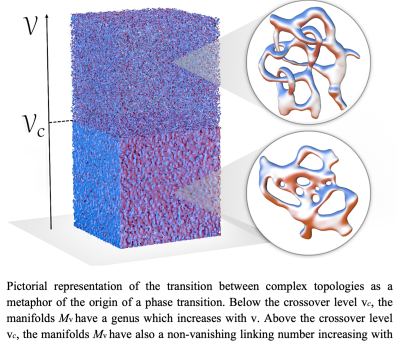
Argomenti di Ricerca
- Transizioni di fase di equilibrio.
- Transizioni di fase di non-equilibrio.
- Ensemble microcanonico.
Un approccio geometrico adeguato allo studio della dinamica dei sistemi classici, semi-classici e quantistici può aprire le porte all'informazione, anche attraverso simulazioni numeriche, altrimenti di difficile accesso. Ad esempio, per un sistema classico isolato a molti corpi, l'ergodicità rende termodinamica e dinamica equivalenti. Pertanto, in questi casi, è possibile misurare grandezze termodinamiche, come temperatura e calore specifico, come medie temporali di opportune funzioni lungo quasi ogni traiettoria di un dato sistema, o, equivalentemente, come un integrale sul suo spazio delle fasi. L'opportunità di passare dalla dinamica alla termodinamica microcanonica e viceversa, offre la possibilità di scegliere il modo più intelligente per misurare una data grandezza.
Argomenti di Ricerca
- Ensemble microcanonico.
- Stati Breather.
- Stati autolocalizzati.
Università di Marsiglia, Politecnico di Torino, Università di Camerino.